This document gives a brief description of the internals of the ICE algorithm. It is assumed that the reader is reasonably familiar with block ciphers, and in particular with DES. If all else fails, the source code may provide a more useful reference.
The algorithm is also described in more detail in a paper presented at the 4th Fast Software Encryption Workshop in Haifa Israel in 1997. However, the paper is only available in postscript form.
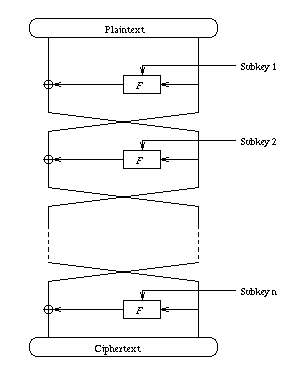
ICE is a standard Fiestel block cipher, as illustrated below. It takes a 64-bit plaintext, which is split into two 32-bit halves. In each round the right half and a 60-bit subkey are fed into the F-function. The output of F is XORed with the left half, then the halves are swapped. This is repeated for all but the final round, where the final swap is left out.
The number of rounds is determined by the level of the variant in use. Level 0 (or Thin-ICE) uses 8 rounds, while higher levels n use 16n rounds.

This is best described by the illustration below.
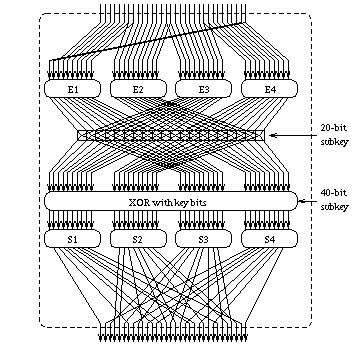
This is very similar to the function used in DES, except for the use of keyed permutation, controlled by a 20-bit subkey in each round. Basically, these 20 bits determine the path that will be taken by the bits leaving E1, E2, E3, and E4. If a bit in the subkey is set, then the corresponding bit from E1 or E2 will be swapped with a bit from E3 or E4 respectively. If the subkey bit is not set, then the bits will continue unimpeded.
This keyed permutation is basically doing the same thing as the salt value in the Unix crypt(3) command, except that the salt here is 20 bits instead of 12, and is derived from the secret key in each round rather than being fixed and publicly known.
The S-boxes take 10-bit inputs and produce 8-bit outputs. The leftmost and rightmost bits of the input are concatenated to produce a 2-bit row selector R. The middle 8 bits form the column selector C. For each row R, there is an XOR offset O and a Galois Field prime P. The 8-bit output of the S-box is given by
under 8-bit Galois Field arithmetic. This is probably better described in the source code, which also lists the 16 XOR offsets and Galois Field primes used to select O and P.
The outputs of the S-boxes are permuted to a 32-bit value via a P-box. The P-box has been designed to maximize diffusion from each S-box, and to ensure that bits which are separated by 16 places never come from that same S-box, nor from S-boxes separated by two places (eg. S1 and S3). Given that these criteria were met, the P-box was also designed to be as regular as possible.
Again, it is probably best to refer to the source for a comprehensive explanation. However, a brief description of the key schedule for the various ICE variants is as follows.